Primeiro de tudo, o que são números primos? Números primos são aqueles que só podem ser divididos por um e por ele mesmo. Esses números são conhecidos há séculos e desempenham um papel essencial na matemática moderna. Nesta postagem, voce vai aprender como eles funcionam, quando e como são usados, além de seus principais benefícios.
Quem não se recorda das lições de aula de matemática ou dos trabalhos escolares sobre isso na escola? Aposto que muita gente ja não se lembra mais, por isso escrevemos este artigo, para ajudar você a se lembrar.
A matemática é uma disciplina que, sem dúvida, aparece no currículo escolar obrigatório e, para aqueles que buscam se destacar, vale a pena estudar alguns conceitos um pouco aprofundados. Saber o que é um número primo e como identificá-lo pode te ajudar na hora de resolver perguntas de matemática nas suas provas de concurso público ou vestibular.
Neste artigo, vamos explicar o que são os números primos e de que forma eles têm influenciado a matemática ao longo dos séculos, bem como por que eles são tão importantes.
O que são números primos?

Os números primos são números inteiros positivos que só podem ser divididos por um e por ele mesmo. Por exemplo, o número 5 é um número primo, pois somente pode ser dividido por 1 e 5. Por outro lado, o número 6 não é primo, pois pode ser dividido por 1, 2, 3 e 6.
Deste de modo, o exemplo citado a cima, sendo o número 5 é considerado um número primo. Nenhum dos divisores, exceto a unidade, podem ser divididos mais uma vez, fazendo com que este número seja chamado de número primo.
O conceito de números primos foi descoberto há séculos atras e reconhecido como matematicamente interessante. Eles não são apenas interessantes do ponto de vista matemático, mas também são usados em diversas áreas, como criptografia, álgebra abstrata, teoria dos números, programação de computadores e muito mais
Mas e o número 1? O número 1 não é considerado um número primo, porque ele pode ser dividido por ele mesmo. Lembre da regra do número primo é que ele seja divisível por ele mesmo e pelo número 1.
História dos números primos
Sua definição é muito antiga e foi tão longe quanto a época dos gregos antigos que pensava sobre isso. Os gregos antigos compreendiam que a divisibilidade dos números estava relacionada às suas estruturas e assim estabeleceram as regras para definir os números primos. Aristóteles foi um dos primeiros a citar explicitamente os tal função e estudou os métodos para determinar se um número era primo ou não.
No século 18, matemáticos como Gauss, Euclides e Fermat perceberam que a identificação dos desses números era mais complicada do que se pensava e começaram a desenvolver métodos para determinar o fator primo efetivamente. Posteriormente, em 1859, o matemático francês Édouard Lucas desenvolveu a ideia de números conhecidos como “números de Lucas”. Este é um método para determinar se um grande número é primo ou composto.
Estudos recentes
Nos últimos anos, os pesquisadores continuaram a estudar para tentar encontrar novo significado sobre o que são os números primos. Por exemplo, Thomas Bloom estimou que existem infinitos números primos. A própria natureza do número primo pode ser usada para prever padrões na natureza.
Além disso, eles também são a base da criptografia, pois os algoritmos de criptografia mais seguros são baseados nesta operação matemática. As chaves seguras usadas para criptografar e descodificar mensagens são formadas a partir de números primos, o que torna extremamente difícil decifrar ou descobrir a chave.
Além disso, as provas importantes sobre a existência de números primos também foram realizadas na teoria dos números. Nesta área, pesquisadores usam conceitos matemáticos comprovados para comprovar se os números são primos ou compostos.
Quais são os critérios para determinar se um número é primo?
Para determinar se um número é primo, você precisa saber os seguintes critérios:
- Todo número primo deve ser maior que 1.
- Um número só pode ser primo se for divisível apenas por 1 e por ele mesmo.
- O número 1 não é considerado primo, pois não é divisível.
Quando e como são usados os números primos?
Os números primos são usados em diversos campos, especialmente na criptografia, a fim de assegurar que informações confidenciais não sejam acessadas por pessoas não autorizadas. Eles possuem muitas aplicações práticas que podem ser aplicados de forma eficiente para varios fins. Eles são usados em criptografia para garantir a segurança da comunicação. Eles também são usados para criar tabelas de verdade, encontrar divisores primos, e descobrir limites e fronteiras.
Por exemplo, os programadores usam métodos de números primos para criar programas de computador que possam detectar erros em sistemas de e-mails, redes sociais ou softwares que requer uma programação complexa.
Além disso, eles são muito usados para estudar problemas matemáticos ainda mais complexos, como o problema da paridade. O problema da paridade pode ser usado para encontrar as condições em que um determinado número é par ou ímpar.
Quais são os números primos de 1 a 100?
Mas como você encontra todos os números primos? Como anotar os mais importantes para a resolução de problemas?
Na verdade, lembrar quais são os números mais importantes na nossa cabeça pode agilizar a resolução das questões em que seja necessária a utilização desses números, mas se você não lembra, existe uma forma prática de se encontrar de forma efetiva os números primos de 1 a 100, que vou te mostrar a seguir.
O método que vai te ajudar a encontrar os números primos de 1 a 100 é chamado de Crivo de Eratóstenes e foi desenvolvido há muitos anos por um matemático grego. Primeiro você tem que escrever todos os números de 1 a 100 em uma folha do seu caderno:
O próximo passo você terá que acompanhar número por número de forma bem prática. Você irá:
- Exceto o número 2, que já é conhecido por ser primo, serrará todos os números pares da tabela. Lembre-se de que todo número par é divisível por 2, portanto não é mais primo.
- Você deve então cortar todos os números divisíveis por 3 (com exceção do próprio numero) de acordo com a regra já explicada no paragrafo acima do nosso artigo..
- Quando você chegar ao número 5, você também deve cortar quaisquer números divisíveis por 5. Observe que, como você já cortou os números pares, a maioria dos números divisíveis por 5 já foram excluídos.
- Finalmente, chegamos ao ultimo passo, que é remover os números que também são divisíveis por 7 da tabela.
Observe que os números primos entre 1 e 100 permanecem na tabela, são eles: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.
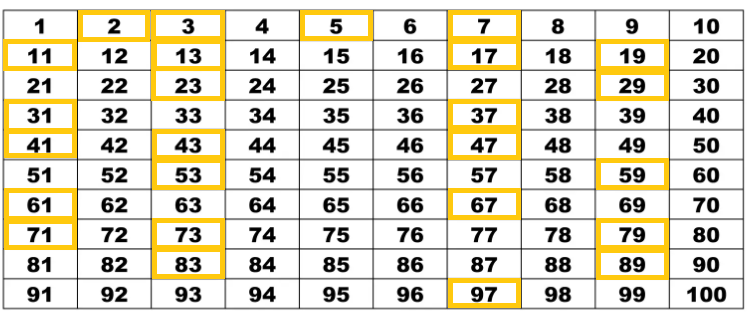
Viu como é fácil! Agora, você sabe um jeito bem mais fácil e efetivo de se resolver as questões das suas provas que constem esse assunto.
Um dos pontos mais impressionantes de todos, é que, à medida que você aumenta os números naturais, fica cada vez mais difícil saber onde estará o próximo número primo. Mas uma fórmula eficaz para encontrá-los não foi descoberta.
Números primos de 1 a 25
Se esta querendo saber quais são os números primos de 1 a 25 eis a resposta!
Você pode encontrara-los facilmente se utilizar o método Crivo de Eratóstenes, sendo assim, os números primos de 1 a 25 são: 2,3,5,7,11,13,17,19,23, como observado na tabela acima
Eles se caracterizam como todos os números naturais podendo ser divididos apenas por 1 e por ele mesmo, como já dissemos acima. Nesse sentido, eles possuem apenas dois divisores.
O conjunto de números entre 1 e 25 compreende: 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25.
Todos esses números se classificam como primos justamente por serem divisíveis apenas por 1 e por eles mesmo.
Qual é o significado dos números primos?
Os números primos desempenham um papel essencial na matemática moderna, pois eles são o alicerce de muitos outros números. Isso significa que, se um número não é primo, então ele pode ser decomposto em números primos. Por exemplo, o número 12 pode ser decomposto em 2 x 2 x 3, que são todos números primos.
Qual é a importância dos números primos?
Os números primos contêm muitos benefícios que são reconhecidos pela ciência e matemática. Em primeiro lugar, eles permitem que você descomponha números complexos em um conjunto de números muito menores para um estudo mais aprofundado. Eles também são fundamentais para a criptografia moderna, pois são usados para gerar números aleatórios que são usados para criptografar dados.
Como podemos usar os números primos para nosso próprio benefício?
Existem várias maneiras de nos beneficiarem em nossas vidas. Por exemplo, podemos usar os números primos para ajudar a resolver problemas de matemática complexos. Além disso, também podemos usa-los para encontrar números que são criptograficamente seguros e que não possam ser facilmente descobertos.
Conclusão
Os números primos são, sem dúvida, importantes para muitos campos de estudo e têm uma história longa e interessante. Esta breve explicação deu uma visão geral sobre tais numeros e de como eles têm influenciado a matemática, bem como suas aplicações práticas.
Se você é um estudante interessado na matemática, vale a pena explorar mais este assunto e descobrir como ele pode te ajudar a se tornar um matemático ainda melhor.
Em suma, eles desempenham um papel importante na matemática moderna. Eles são essenciais para a criptografia, pois gerenciam informações confidenciais. Além disso, vimos que eles também são usados para descompô-los em seus componentes mais elementares para um estudo mais profundo e também para gerar números aleatórios.
Por último, você também pode usar os números primos para seus próprios benefícios, ajudando a resolver problemas matemáticos complexos e descobrindo números seguros para criptografia. Compartilhe esta informação em suas redes sociais para que mais pessoas possam saber o que são números primos e como eles podem ser usados.
Compartilhe em suas redes sociais o que você aprendeu aqui hoje além disso, você também pode deixar sua duvida aqui nos comentários.





















